1.3. Meets and Joins#
from IPython.display import Image

See also Join and meet. It’s hard to remember these terms; for people to “meet” simply means that they come together and for objects to “join” also means they simply come together. Like conjunction and disjunction, the words don’t really indicate that one option is better or worse. The author tries to comment on terminology at the bottom of Example 1.87, which only helps a bit.
One way to remember is to say them in order of low to high, just like you would list numbers (0,1,2,3 …). In that case you’d want to say “meet and join” rather than “join and meet” as Wikipedia does. Unfortunately that’s not also alphabetical order (like conjunction and disjunction). Another reason to say “meets and joins” rather than “join and meet” is that limits correspond to meets and colimits to joins, and we’ll almost always say “limits and colimits” rather than “colimits and limits” when we’re on that topic. Also, MJ was a famous basketball player and this section is on page 23.
See also Infimum and supremum; these are also in alphabetical order unlike meet and join. These words are essentially synonyms to meet and join; there’s no indication of any difference in either article. The best language is GLB and LUB (again, properly in alphabetical order), though these are also the wordiest.
1.3.1 Definition and basic examples#

Exercise 1.80#
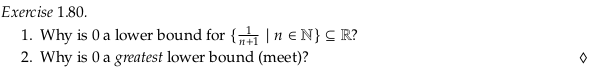
Image('raster/2023-10-07T13-43-47.png', metadata={'description': "7S answer"})
Show code cell output
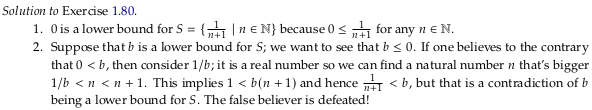
Definition 1.81#



Search Meet and join (not plural); consider making a redirect for “meets and joins” as well, which makes sense to search given multiple (isomorphic) meets and joins may exist.
Exercise 1.85#

For 1., we have that for all \(a \in A\) (only one element) we have \(p \leq a\), satisfying the first
requirement. The second requirement is that for all \(q\) such that \(q \leq a\) for all \(a \in A\), we
have that \(q \leq p\). This requirement allows for other \(q\) that are equivalent to \(p\).
In 2. we remove the possibility of equivalent sets of elements by making the preorder skeletal.
The answer to 3. is yes.
Reveal answer



Exercise 1.90#

The meet is the greatest common divisor and the join is the least common multiple.
Reveal answer



1.3.2 Back to observations and generative effects#

Exercise 1.94#

There are only two possible worlds to consider; that \(a \leq b\) or that \(b \leq a\). If the first is true, then by the definition of \(f\) as a monotone map we have that \(a \leq_P b\) implies \(f(a) \leq_Q f(b)\). This implies the expression \(f(a) \vee f(b)\) is equivalent to \(f(b)\), which is \(\leq\) the expression \(f(a \vee b) = f(b)\). If the second case (\(b \leq a\)) is true, then again by the definition of a monotone map we have that \(b \leq a\) implies \(f(b) \leq f(a)\), the left hand expression is \(f(a)\), and the right hand expression is \(f(a \vee b) = f(a)\).
Reveal answer

