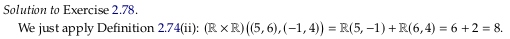2.4. Constructions on 𝓥-categories#
from IPython.display import Image

2.4.1. Changing the base of enrichment#



Exercise 2.67#
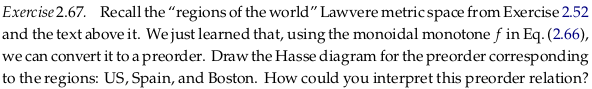
You could interpret this preorder as a “contains” or “includes” relationship (the US contains Boston).
Reveal 7S answer

Exercise 2.68#

For 1., define g to be the second monoidal monotone we looked at in Exercise 2.44 (called \(u(x)\)
in that question).
For 2. we can use the same Lawvere metric space from Exercise 2.67. The new Bool-category:
Reveal 7S answer

2.4.2. Enriched functors#

This definition is definitely not enough to understand Enriched category § Enriched functors. If you have read ahead enough to understand that functors preserve identity and composition, you can see this as a statement that these are preserved. If previously there was a morphism between x₁ and x₂ (in a Bool-category, one is less than the other), then a functor must map this morphism to another morphism between F(x₁) and F(x₂) in a second Bool-category that respects composition.
The ⊗ operator serves as the associative operator connected to the enriched category (that emulates the composition of morphisms). For the enriched functor to respect the enriched structure means for it to respect the structure that the category includes beyond just identity and associativity: in this case Definition 2.2. defines in e.g. (a), (b), and (d) some additional structure that might need to be preserved.


See also Lipschitz continuity.
Exercise 2.73#

A Cost-category is a Lawvere metric space. When we add the “skeletal” adjective (i.e. property/constraint), we satisfy condition (b) in Definition 2.51. When we add the “dagger” adjective, we satisfy condition (c) in Definition 2.51, satisfying everything we need for the definition of an extended metric space.
For 2., notice the symmetry in the statements:
A skeletal dagger preorder is a set.
A skeletal dagger Lawvere metric space is an extended metric space.
See also Dagger category.
Reveal 7S answer

2.4.3. Product 𝓥-categories#


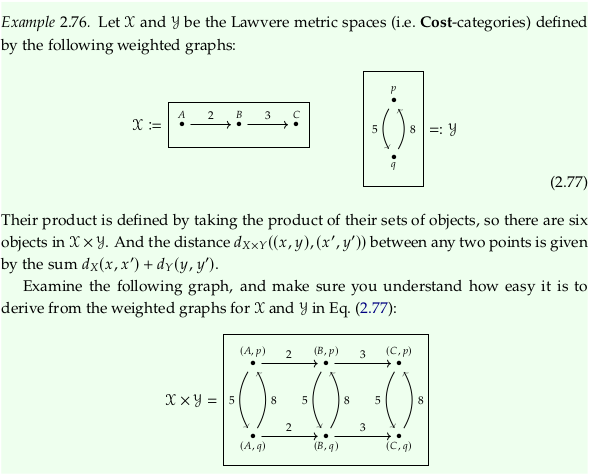
Exercise 2.75#

For 1.:
Using property (a) in Definition 2.2, we can assert this statement is true because \(I \leq \cat{X}(x,x)\) and \(I \leq \cat{Y}(y,y)\).
For 2.:
Using property (a) in Definition 2.2, we can assert this statement is true because:

Reveal 7S answer

Exercise 2.78#
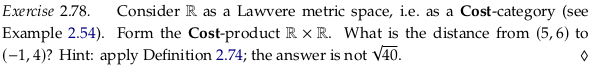
Forming the non-obvious part of the Cost-product:
So the answer should be \(|5 - -1| + |6 - 4| = 8\).
Reveal 7S answer