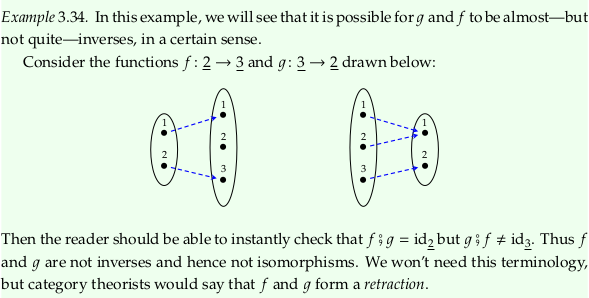
3.2. Categories

For a similar definition, see Category (mathematics). It excludes (iii), but makes a note that some authors include it. This page also provides a long list of examples, similar to what this section will do.

As noted in Morphism, some people also prefer to use “hom-class” for what is called “hom-set” here.

Thinking only in terms of sets and functions is limiting. What if all the items in your set share some property that you want maintain (or transform) as part of the functions associated with it? For example, groups have several definining properties and group homomorphisms maintain them. This is where category theory begins.

You can come to nearly the same perspective by thinking in terms of the elements/examples in the set you care about as training examples. What properties do the elements have in common that makes them belong to the same “set” so to speak? If you’re going to do any work on your training examples then you need to understand these properties and be careful about how you maintain or transform them. That is, you can’t just apply any functions to them.

3.2.1. Free categories

Compare to Free category.

Exercise 3.9.

The unitality condition is satisfied because concatenating (composing) with identities at any vertex does nothing. The associativity property is satisfied because concatenating arrows should lead to the same path regardless of which arrows you concatenate first.

Reveal 7S answer

Exercise 3.10.

For 1.:

For 2., the identities only show up in the resulting table as an identity matrix where the same identities line up. The identities can only be concatenated with themselves.

Reveal 7S answer

Exercise 3.12.

The category 1 would have only object v₁ for the one vertex, and one morphism id₁ for it’s identity morphism.

The category 0 would have the empty set for both its collection of objects and all hom-sets between objects (of which there are none).

You’d have n identify morphisms, max(0, n-1) length-one morphisms, max(0, n-2) length-two morphisms, etc. The pattern may be more familiar when the calculations are written out:

|hom(0)| = 0
|hom(1)| = 1
|hom(2)| = 2 + 1
|hom(3)| = 3 + 2 + 1
|hom(4)| = 4 + 3 + 2 + 1

This is an arithmetic series; the formula for the nth term is n(n+1) / 2.

Reveal 7S answer

Example 3.13.

Exercise 3.15.

The addition of the two numbers.

Reveal 7S answer

3.2.2. Presenting categories via path equations

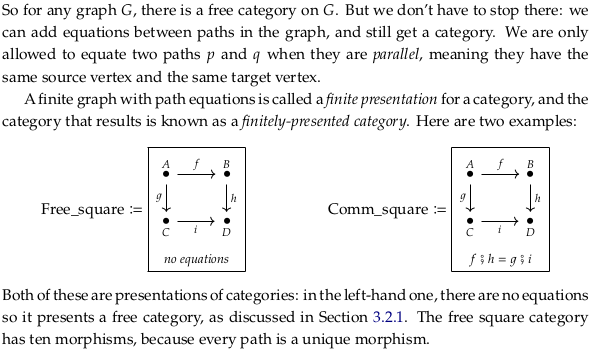
We present categories with a set of “generators” and equations, analogous to the Presentation of a group.

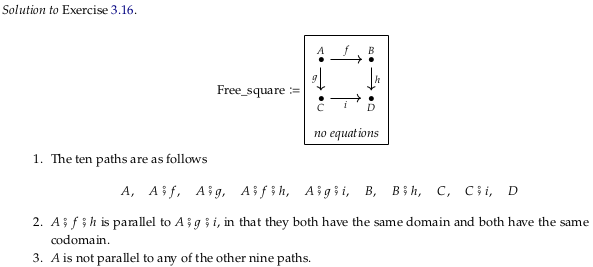
Exercise 3.16.

The ten paths are A, B, C, D, f, g, h, i, hf, and ig. The hf and ig paths are parallel. The f and i paths are not parallel.

Reveal 7S answer

Exercise 3.17.

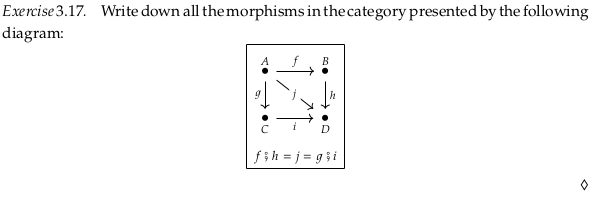
A, B, C, D, f, g, h, i, j

Reveal 7S answer

Exercise 3.19.

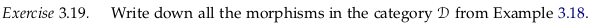
z
s = z;s = s;z
s;s = s;s;s;s = z;s;s = s;s;z
s;s;s = z;s;s;s = s;s;s;z = s;s;s;s;s

Reveal 7S answer

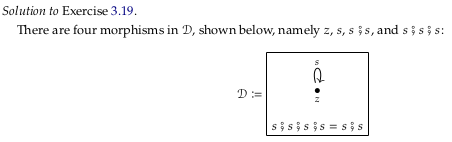
The author’s answer seems wrong; he claims the morphisms are “shown below” and then reproduces the same drawing from Example 3.18.

3.2.3. Preorders and free categories: two ends of a spectrum

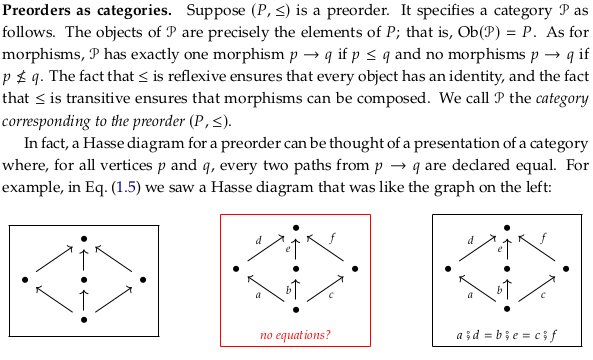
Exercise 3.21.

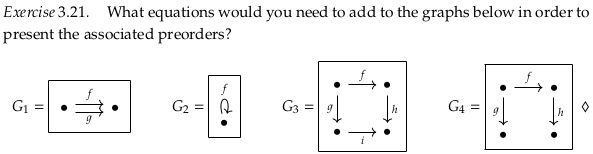
G₁ would need f = g. G₂ would need id = f. G₃ would need hf = ig. G₄ would not need anything.

Reveal 7S answer

Exercise 3.22.

The discrete preorder with one element.

Reveal 7S answer

3.2.4. Important categories in mathematics

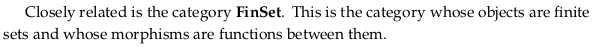
Exercise 3.25.

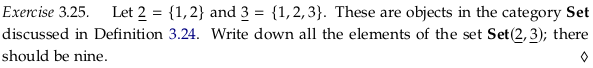
Representing the unary function as a binary relation:

(1,1), (2,1)
(1,1), (2,2)
(1,1), (2,3)
(1,2), (2,1)
(1,2), (2,2)
(1,2), (2,3)
(1,3), (2,1)
(1,3), (2,2)
(1,3), (2,3)

Reveal 7S answer

3.2.5. Isomorphisms in a category

Exercise 3.30.

For 1., define f⁻¹(2) = a, f⁻¹(1) = b, f⁻¹(3) = c. For 2. in general there are same as the number of permutations of the set (n!), in this case 6.

Reveal 7S answer

Exercise 3.31.

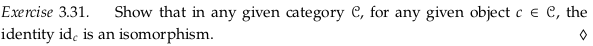
The identity idₘ for the object m always has an inverse, namely itself (idₘ).

Reveal 7S answer

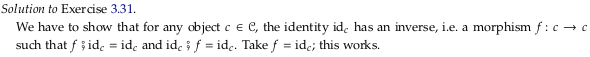
Exercise 3.32.

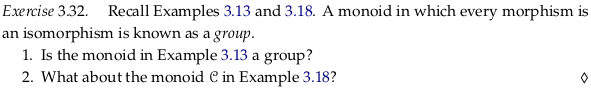
The monoid in Example 3.13 is not a group because \(s\) does not have an inverse.

Both the monoids in Example 3.18 are a group. The first is a group because the inverse of \(z\) is \(z\), and the inverse of \(s\) is \(s\). The second is a group because the inverse of \(z\) is \(z\), the inverse of \(s\) is \(s;s;s\), the inverse of \(s;s\) is \(s;s\), and the inverse of \(s;s;s\) is \(s\).

Reveal 7S answer

Exercise 3.33.

Consider the graph with only vertices m and n, and with arrows in both directions between m and n (call them f and g). It is not the case that f;g = idₘ and g;f = idₙ; these are additional equations that would violate the condition of this being a free group. Rather, f;g and g;f are additional morphisms in the hom-sets hom(f,g) and hom(g,f) (which are infinite sets).

Reveal 7S answer