10. Galois theory#
10.1 The big question#
Compare Field (mathematics) to Definition 10.1.
Compare the author’s definition of polynomial equation to Algebraic equation.
Regarding the discovery in 1824 by Niels Abel, see Abel–Ruffini theorem. Galois worked from 1828-1832.
10.2 More big questions#
See Number § Main classification for an even finer classification of the types of numbers.
Compare Key Point 10.5 and the surrounding paragraphs to Galois theory § Application to classical problems.
10.3 Visualizing field extensions#
Compare the first paragraph of this section to Field extension.
Compare Theorem 10.3 to Complex conjugate root theorem.
10.4 Irreducible polynomials#
Compare to Irreducible polynomial.
Compare Theorem 10.4 to Eisenstein’s criterion:
Suppose we have the following polynomial with integer coefficients:
\[ Q(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 \]If there exists a prime number p such that the following three conditions all apply:
\(p\) divides each \(a_i\) for \(0 ≤ i < n\),
\(p\) does not divide \(a_n\), and
\(p^2\) does not divide \(a_0\),
then \(Q\) is irreducible over the rational numbers.
The definitions are essentially equivalent, except the author combines the first two bullet points into one.
10.5 Galois groups#
All the examples in this section seem to be rather standard, as Field extension § Examples covers them as well. The second and third are also covered in the Fundamental theorem of Galois theory examples.
Per Field extension § Extension field, \(ℚ(S)\) should be read “\(ℚ\) adjoin \(S\)” where \(S\) is a set that we want to adjoin to \(ℚ\). The purpose of these examples is to confirm that the field generated by adjoining e.g. the set \(\{\sqrt{2},\sqrt{3}\}\) to \(ℚ\) is still a field, or if we need more elements (for it to be closed). This is not a complete Algebraic closure of the field, which would include all algebraic numbers (e.g. the algebraic closure of the rationals is the algebraic numbers). It appears the correct name for this is a Normal extension § Normal closure.
10.5.1 A small field extension ℚ(√2)#
This example is a Simple extension, because it only adds one element. The next can also be seen as simple despite the fact that it appears to add two elements, as discussed in Field extension § Examples. This doesn’t prevent it from having degree four, however. This first example differs from the next in being a Quadratic field, however.
Compare Degree of a field extension, which highlights the valuable interpretation of extensions fields (which are just fields) as vector spaces. The author’s suggestion to always view subtraction as the addition of a negative element (below Figure 10.1) is particularly appropriate in this view. We can see elements of \(ℚ(\sqrt{2})\) of the form \(a + b\sqrt{2}\) as vectors \([a,b]\) in a vector space of dimension 2 over \(ℚ\). Similarly, we can see elements of \(ℚ(\sqrt{2},\sqrt{3})\) of the form \(a + b\sqrt{2} + c\sqrt{3} + d\sqrt{6}\) as vectors \([a,b,c,d]\).
For example, we often visualize a Gaussian rational, Gaussian integer, or complex number as having a place on a 2-D plane (the Complex plane). See Algebraic number field § Examples.
Compare Theorem 10.5 to the following from Field extension § Algebraic extension:
An element \(s\) of \(L\) is algebraic over \(K\) if and only if the simple extension \(K(s)/K\) is a finite extension. In this case the degree of the extension equals the degree of the minimal polynomial, and a basis of the \(K\)-vector space \(K(s)\) consists of \(1,s,s^2,\dots,s^{d-1}\) where \(d\) is the degree of the minimal polynomial.
10.5.2 The symmetries of ℚ(√2)#
The author’s approach in this section is similar to that of Galois theory § Permutation group approach. This is apparently how Galois originally approached the problem.
See the following from Galois theory § Quadratic equation:
If the polynomial has rational roots, for example \(x^2 - 4x + 4 = (x - 2)^2\), or \(x^2 - 3x + 2 = (x - 2)(x - 1)\), then the Galois group is trivial; that is, it contains only the identity permutation. In this example, if *\(A = 2\) and \(B = 1\) then \(A - B = 1\) is no longer true when \(A\) and \(B\) are swapped.
It’t not clear that the first example is correct here (the one with a root of multiplicity two). It seems like a repeated root would lead to some symmetry (🔨).
Compare Definition 10.6 to Galois group § Definition:
Suppose that \(E\) is an extension of the field \(F\) (written as \(E/F\) and read “\(E\) over \(F\)”). An automorphism of \(E/F\) is defined to be an automorphism of \(E\) that fixes \(F\) pointwise. In other words, an automorphism of \(E/F\) is an isomorphism \(α: E → E\) such that \(α(x) = x\) for each \(x ∈ F\). The set of all automorphisms of \(E/F\) forms a group with the operation of function composition. This group is sometimes denoted by \(Aut(E/F)\).
If \(E/F\) is a Galois extension, then \(Aut(E/F)\) is called the Galois group of \(E/F\), and is usually denoted by \(Gal(E/F)\).
This definition doesn’t quite match the authors, which is discussed at the end of section 10.5.3.
10.5.3 Symmetries of field extensions#
Compare to the following from Automorphism § Examples:
A field automorphism is a bijective ring homomorphism from a field to itself.
The field ℚ of the rational numbers has no other automorphism than the identity, since an automorphism must fix the additive identity 0 and the multiplicative identity 1; the sum of a finite number of 1 must be fixed, as well as the additive inverses of these sums (that is, the automorphism fixes all integers); finally, since every rational number is the quotient of two integers, all rational numbers must be fixed by any automorphism.
…
The study of automorphisms of algebraic field extensions is the starting point and the main object of Galois theory.
To be clear, the three groups the author is referring to at the end of this section are:
The “Galois group” according to Definition 10.6, meaning the domain of an isomorphism \(ψ\) from the “Galois group” to permutations of the roots of a polynomial.
The codomain of \(ψ\) i.e. the permutations of the roots of a polynomial that are undetectable by equations of arithmetic (which form a permutation group).
The “Galois group” according to Galois group § Definition is the group of all field automorphisms \(ϕ\). These field automorphisms \(ϕ\) are much “bigger” in some sense than the \(ψ\) because they switch not only the roots but all the elements of a field (other than the elements fixed by the automorphism).
The author does not consistently use one definition, as we’ll see below. Neither do authors on Wikipedia; see this use of the term in Galois theory § Permutation group approach:
These permutations together form a permutation group, also called the Galois group of the polynomial, which is explicitly described in the following examples.
10.5.4 The symmetries of ℚ(√2,√3)#
Compare Theorem 10.7 to Degree of a field extension § The multiplicativity formula for degrees.
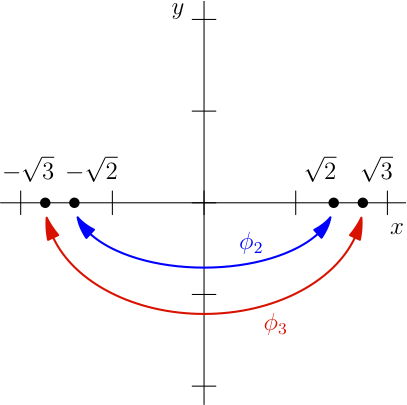
In the caption of Figure 10.12, the author refers to the automorphism group as the Galois group. The Wikipedia article Galois group § Definition would refer to this as the Galois group, but strictly speaking the author’s Definition 10.6 would not call this the Galois group.
From the errata (⚠️):
Page 241, Figure 10.13: The figure uses red and blue backwards. In order to be consistent with Figure 10.12, the red should be blue and vice versa. Here is a corrected version.
Recall how the degree of an extension \(E/F\) is equivalent to the dimension of a vector space over \(F\). This suggests that we could visualize elements of the field extension \(ℚ(\sqrt[3]{2}\) in three dimensions, which would be perfectly possible. In the imaginary plane we can add imaginary numbers, and we could do the same in this space. The utility is a bit limited when it comes to multiplication however; in the imaginary plane we can see multiplication as a rotation, but there isn’t anything quite equivalent in every field extension.
10.5.5 The symmetries of ℚ(∛2)#
From the errata (⚠️):
Page 242, line 6: The phrase “neither \(r_1\) nor \(r_2\)” should be “neither \(r_2\) nor \(r_3\).”
Compare the author’s defintion of normal extension to Normal extension. In fact, Normal extension § Examples and counterexamples addresses this example specifically and suggests how to more generally (for any prime) perform the normal closure the author also performs. Notice \((\sqrt[3]{2})^2 = \sqrt[3]{4}\).
Compare Theorem 10.9 to the following from Fundamental theorem of Galois theory § Properties of the correspondence:
Degrees of extensions are related to orders of groups, in a manner consistent with the inclusion-reversing property. Specifically, if \(H\) is a subgroup of \(Gal(E/F)\), then \(|H| = [E:E^H]\) and \(|Gal(E/F)|/|H| = [E^H:F]\).
10.6 The heart of Galois theory#
Compare Theorem 10.10 to the Fundamental theorem of Galois theory.
Compare Theorem 10.11 to Solvable group § Definition.
From the errata (⚠️):
Page 246, Figure 10.20: The subgroups in the figure marked as \(V_4\) should be marked as \(C_4\) instead. Furthermore, the equality signs in the figure are incorrect; the groups are isomorphic, not equal. (The congruence sign should be used instead.)
10.7 Unsolvability#
10.7.1 An unsolvable group#
From the errata (⚠️):
Page 249, paragraph above 10.7.2: The following sentence is inaccurate:
Furthermore, no group containing \(A_5\) can be solvable, because the smallest first step in any chain of normal subgroups in such a group would be the invalid step \({e} ⊲ A_5\).
It should be rewritten along the following lines:
Furthermore, no group containing \(A_5\) can be solvable. No step \(A ⊲ B\) in such a chain can have the quotient \(B/A\) isomorphic to \(A_5\), because it is not abelian. And yet it can also be shown that a step in the chain including just “part” of \(A_5\) could be used to reveal a normal subgroup in \(A_5\), an impossibility.
10.7.2 An unsolvable polynomial#
The author claims:
The Galois group must also contain the complex conjugacy automorphism, as all Galois groups do. How this automorphism permutes the five roots depends on how many of those roots are real numbers.
This statement is potentially confusing because the complex conjugacy automorphism can be trivial. For more details, see Complex conjugation in the Galois group of a polynomial - MSE.
See Proving that a polynomial is not solvable by radicals. - MSE for almost the same logic as the author’s applied to a similar polynomial; it also suggests a shorter solution using a different theorem.
Avoiding unnecessary solutions#
It may seem “unsatisfying” to only refer to the roots \(\{r_1,r_2,\dots,r_5\}\) via variable names. Is the solution \(\frac{-b±\sqrt{b^2-4ac}}{2a}\) much better, though? It may be what we’re used to, but it’s really not that simple or satisfying. Expressing the solution to cubic equations is a practical nightmare (try it in Exercise 10.7 part (c)).
If it wasn’t for radicals being invented, we could have referred to the solutions to e.g. \(3x^2 + x + 1\) without having to write them out (which takes more space than “the solutions to \(3x^2 + x + 1\)”). If it’s more satisfying to refer to it symbolically, then define \(f(x) = 3x^2 + x + 1\) and refer to \(f^{-1}(0)\) (the kernel of \(f\), see Zero of a function).
Solutions beyond radicals#
See comments at the bottom of The Cubic Formula for a helpful perspective on this result; it also suggests another way to solve a quintic is via the inverse of the function \(f(x)=x^5+x\). The section Quintic function § Beyond radicals suggests solutions in terms of elliptic functions, as well as Algebraic equation § Higher-degree equations. Per Why do we make such big deal about the ‘unsolvability’ of the quintic? - MO we can solve the cubic equation with trigonometric functions rather than radicals, as discussed in Cubic equation § Trigonometric and hyperbolic solutions.