Exercise 7.4

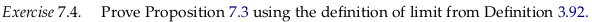
Taking morphism labels from Wikipedia:

We’ll take rt to mean r∘t, as in the Wikipedia article, for brevity. We’ll break the problem into part 1. where we show that if the left square is a pullback then the whole rectangle is a pullback and part 2. where we show the converse.

For part 1., if the left square is a pullback, then for any other cone \((Q,q_1,q_2)\) over \(A'→B'←B\) there is some unique morphism \(k: Q→A\) such that \(k\) factors out of the pair of maps \(q_2: Q→B\) and \(q_1: Q→A'\). That is, we have that \(q_2 = t∘k\) and \(q_1 = u∘k\). The \(Q,q_1,q2\) variable names are coming from Pullback (category theory).

Take some arbitrary (in the sense of ∀, see Glossary of mathematical jargon § Descriptive informalities) third morphism \(q_3: Q→C\) where \(f∘q_3 = g∘h∘q_1\) to come up with an arbitrary cone \((Q,q_1,q_3)\) over \(A'→C'←C\). A picture to have in mind is:

Is there always a unique morphism from \((Q,q_1,q_3)\) to \((A,rt,u)\)? We know that \(k\) is a good candidate because \(q_1 = u∘k\). Is it also always the case that \(q_3 = l∘k\) for some morphism \(l\)?

Because the right square is a pullback, \((B,r,s)\) is the limit with respect to the cospan \(B'→C'←C\). We know that \((Q,h∘q_1,q_3)\) is also a cone over \(B'→C'←C\), so we have that \(q_3 = r∘q_2\). Given \(q_2 = t∘k\) (see above) we then have that \(q_3 = r∘t∘k\) and so \(l = r∘t\) and \(k\) can serve as the unique morphism from \((Q,q_1,q_3)\) to \((A,rt,u)\). This makes the limit of f and gh equal \((A,rt,u)\), which is what we wanted to show.

For part 2. we assume that the whole rectangle is a pullback and must show that the left rectangle is a pullback as well.

Because the whole rectangle is a pullback, then for any other cone \((Q,q_1,q_3)\) over \(A'→C'←C\) there is some unique morphism \(k: Q→A\) such that \(k\) factors out of the pair of maps \(q_3: Q→C\) and \(q_1: Q→A'\). That is, we have that \(q_3 = r∘t∘k\) and \(q_1 = u∘k\).

Take some arbitrary third morphism \(q_2: Q→B\) where \(s∘q_2 = h∘q_1\) to come up with an arbitrary cone \((Q,q_1,q_2)\) over \(A'→B'←B\). Is there always a unique morphism from \((Q,q_1,q_2)\) to \((A,t,u)\)? We know that \(k\) is a good candidate because \(q_1 = u∘k\). Is it also always the case that \(q_2 = m∘k\) for some morphism \(m\)?

Because the right square is a pullback, \((B,r,s)\) is the limit with respect to the cospan \(B'→C'←C\). We know that \(g∘h∘q_1 = f∘q_3\) and we have that \(g∘h∘q_1 = g∘s∘q_2\) because \(h∘q_1 = s∘q_2\), so \(g∘s∘q_2 = f∘q_3\). So \((Q,s∘q_2,q_3)\) is also a cone over \(B'→C'←C\), so we have that \(q_3 = r∘q_2\). Given \(q_3 = r∘t∘k\) (see above) we then have that \(q_2 = t∘k\) so \(m = t\) and \(k\) can serve as the unique morphism from \((Q,q_1,q_2)\) to \((A,rt,u)\). This makes the limit of s and h equal \((A,t,u)\), which is what we wanted to show.