6.5 Operads and their algebras

6.5.1 Operads design wiring diagrams

See also Operad.

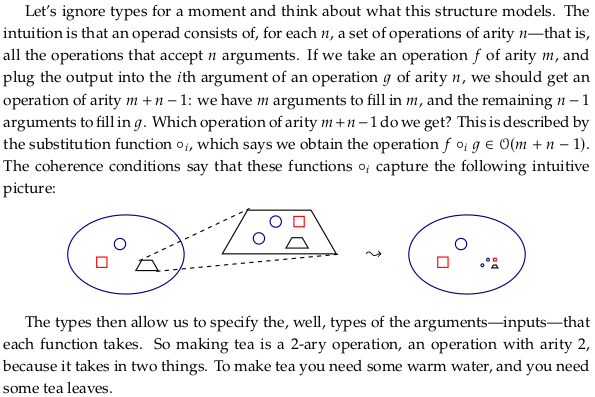
See also Context-free grammar.

6.5.2 Operads from symmetric monoidal categories

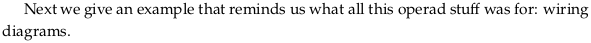
Exercise 6.96

For part 1.:

For part 2.:

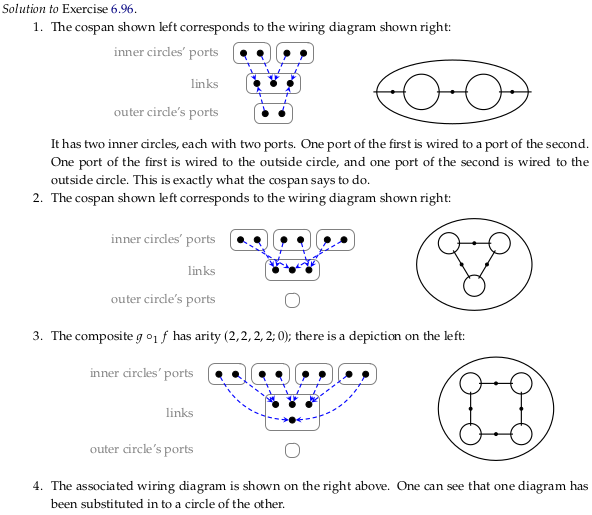
For part 3. see part (iii) of Rough Definition 6.91, which is more detailed than part (iii) of Example 6.94. In this case we have \(i=1\). The variable \(i\) can be interpreted as “the index where we want to substitute the first tuple” (assuming the variable \(s\) is used to mean “substituted”) so that:

\[ ∘_1: 𝓞(s_1,...,s_m;t_1)×𝓞(t_1,...,t_n;t)→𝓞(s_1,...,s_m,t_2,...,t_n;t) \]

We’ll have to assume:

\[\begin{split} \begin{align} f & ∈ 𝓞(s_1,...,s_m;t_1) = \textbf{Cospan}(2,2;2) \\ g & ∈ 𝓞(t_1,...,t_n;t) = \textbf{Cospan}(2,2,2;0) \end{align} \end{split}\]

So that:

\[ \begin{align} g ∘_1 f ∈ 𝓞(s_1,...,s_m,t_2,...,t_n;t) = \textbf{Cospan}(2,2,2,2;2) \end{align} \]

We must make this assumption because the definition in part (iii) of Definition 6.91 is unclear about order, and because the opposite substitution just doesn’t work. This assumption also fits Example 6.93, where the author is also using the variable names \(f\) and \(g\) (suggesting that is also what he is looking at). In Example 6.93, notice the author flips the order of \(f\) and \(g\) between the equation that defines \(g ∘_i f\) and the sentence below it.

Turning the cospans on their sides to compute the composite in the connected-components style of (6.47) (and adding colors only to help visually distinguish connected components):

For part 4.:

Reveal 7S answer

Definition 6.97

6.5.3 The operad for hypergraph props