2.2. Symmetric monoidal preorders#
from IPython.display import Image

2.2.1. Definition and first examples#
Definition 2.2.#


Define monoidal preorder#
See also Monoidal category - Monoidal preorders for an alternative definition of non-symmetric monoidal preorders. The full definition of a Monoidal category is not introduced (even roughly) until section 4.4.3.
You can remember the term “monoidal product” for the ⊗ operator because in general the “most important” example of a monoid in this context is going to be the real numbers with multiplication as the ⊗ operator. The usual formula for matrix multiplication (and by extension, for dot products) is based on this monoid; see Section 2.5.3. However, the symbol ⊗ (\otimes or “circled times”) is primarily associated with the Tensor product (see The Tensor Product, Demystified) and is the original source of this word. A final option is to associate this word to the “Cartesian product” when you are working with Set-categories (regular categories) (see Example 4.49).
In the short term we’re going to have to accept “+” as a “monoidal product” however. The article Monoid tries to avoid anything but the language “binary operator” in its definition.
Definitional variation#
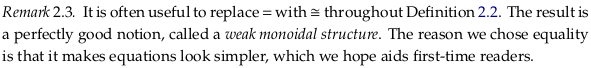
Notational variation#

Example 2.4.#

Exercise 2.5.#

See also Exercise 2.5.
Image('raster/2023-10-28T17-43-10.png', metadata={'description': "7S answer"})
Show code cell output
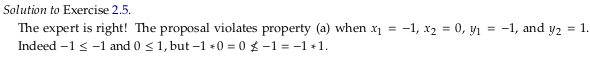

Exercise 2.8.#

See also Exercise 2.8.
Image('raster/2023-10-28T17-43-36.png', metadata={'description': "7S answer"})
Show code cell output

Example 2.9.#

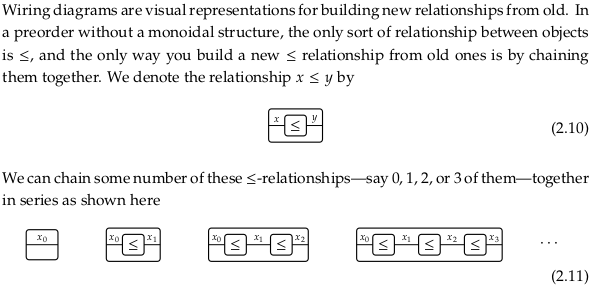
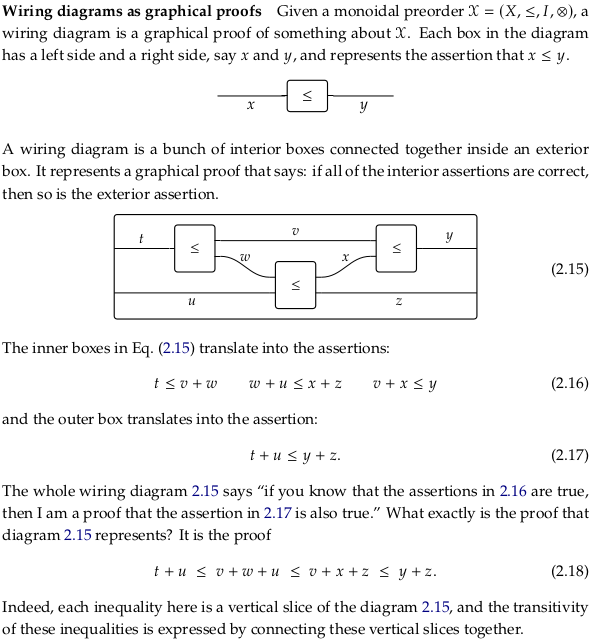
2.2.2. Introducing wiring diagrams#
Compare to String diagram and string diagram in nLab.


See also the concept of a “valid” argument in Chapter 3 Other logical notions ‣ Part I Key notions of logic ‣ forall x: Calgary.




Exercise 2.20.#

See also Exercise 2.20.
Image('raster/2023-10-28T17-44-37.png', metadata={'description': "7S answer"})
Show code cell output


2.2.3. Applied examples#

Chemistry#
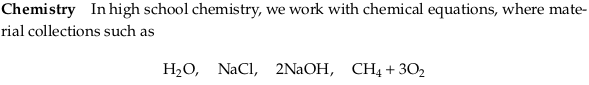

Exercise 2.21.#
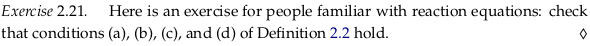
See also Exercise 2.21.
Image('raster/2023-10-28T18-07-23.png', metadata={'description': "7S answer"})
Show code cell output


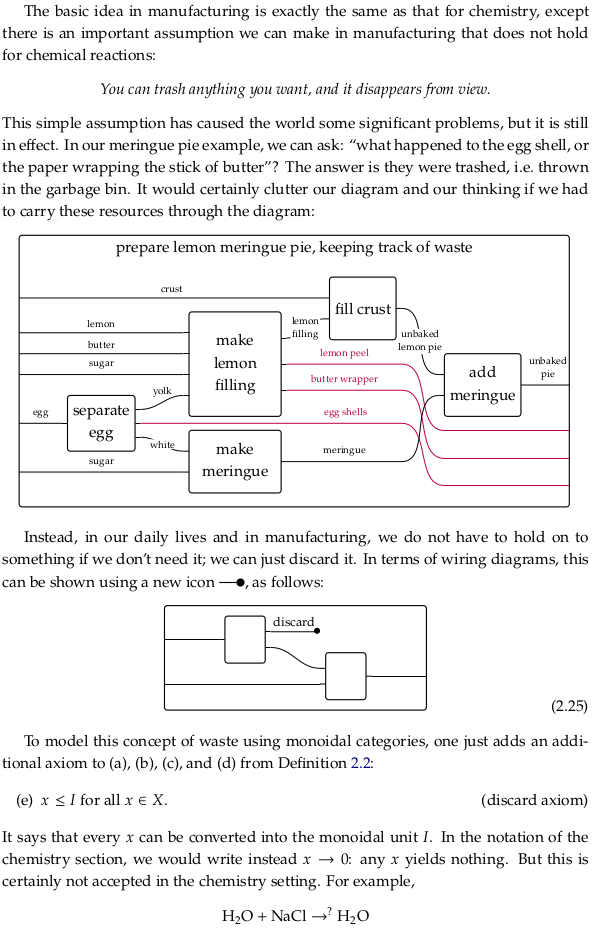
Manufacturing#


Informatics#
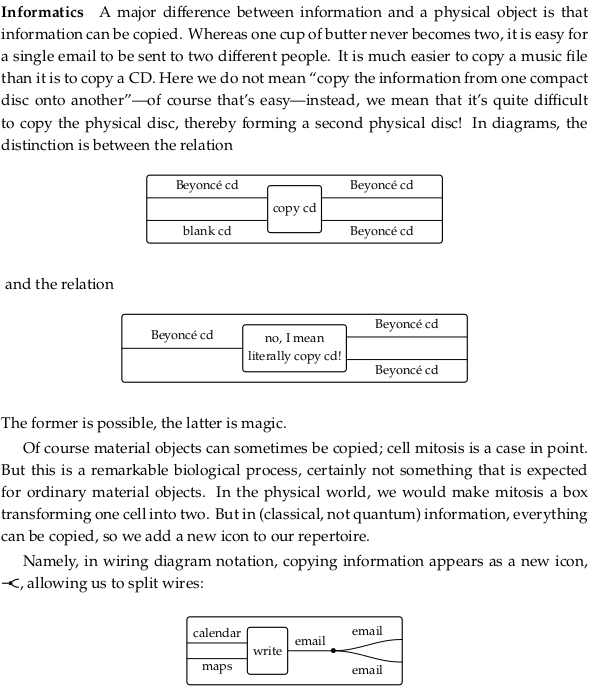
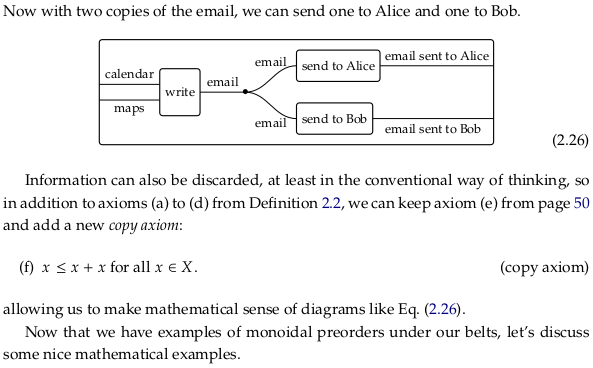
2.2.4. Abstract examples#



Exercise 2.29.#

See also Exercise 2.29.
Image('raster/2023-10-28T18-08-22.png', metadata={'description': "7S answer"})
Show code cell output


Exercise 2.31.#
Notice this question only asks for a monoidal structure, not a symmetric monoidal preorder structure. Since it seems to have both, we’ll show both here.
The monoidal unit should be 1 (satisfies unitality). The natural numbers under addition satisfy the associativity condition, so this symmetric monoidal preorder will as well. See Natural number - Algebraic properties satisfied by the natural numbers. The natural numbers also satisfy the commutativity condition (symmetry condition in the text).
The following is based (roughly) on Propositional calculus § Natural deduction system and Propositional calculus § Proofs in propositional calculus. To see the monotonicity condition is satisfied we’ll use the normal rules of algebra on the natural (positive) numbers, with these two premises:
We have, multiplying both sides of the first premise by \(y_2\):
Multiplying both sides of the second premise by \(x_1\):
And combining the last two equations with transitivity:
Image('raster/2023-10-28T18-10-26.png', metadata={'description': "7S answer"})
Show code cell output


Exercise 2.33.#

See also Exercise 2.33.
Image('raster/2023-10-28T18-10-52.png', metadata={'description': "7S answer"})
Show code cell output
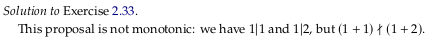
Exercise 2.34.#

See also Exercise 2.34.
Image('raster/2023-10-28T18-12-02.png', metadata={'description': "7S answer"})
Show code cell output

See also Exercise 2.29; we could have constructed a NMY preorder from the max operation as well.
Exercise 2.35.#
See also Exercise 2.35.

Image('raster/2023-10-28T18-12-44.png', metadata={'description': "7S answer"})
Show code cell output
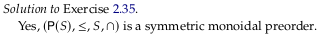
Exercise 2.36.#
See also Exercise 2.36.

Image('raster/2023-10-28T18-13-36.png', metadata={'description': "7S answer"})
Show code cell output


Example 2.37#

See also Extended real number line (which adds both a +∞ and -∞).

Exercise 2.39.#
See also Exercise 2.39.

Image('raster/2023-10-28T18-14-01.png', metadata={'description': "7S answer"})
Show code cell output

Exercise 2.40.#
See also Exercise 2.40.
Image('raster/2023-10-28T18-15-01.png', metadata={'description': "7S answer"})
Show code cell output
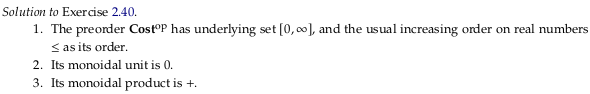
2.2.5. Monoidal monotone maps#
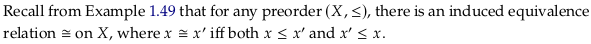




Exercise 2.43#
See also Exercise 2.43.

Image('raster/2023-10-28T18-15-36.png', metadata={'description': "7S answer"})
Show code cell output

Exercise 2.44#
See also Exercise 2.44.

Image('raster/2023-10-28T18-15-59.png', metadata={'description': "7S answer"})
Show code cell output

Exercise 2.45#
See also Exercise 2.45.

Image('raster/2023-10-28T18-17-16.png', metadata={'description': "7S answer"})
Show code cell output
