Exercise 7.32#

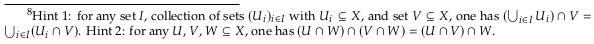
See also Subspace topology. The author refers to an arbitrary open set of \(X\) as \(B\), and of \(Y\) as \(A\). Keep this flip in mind; we think of \(X\) ≤ \(Y\) (alphabetically) but this doesn’t match \(A\) ≤ \(B\). The Wikipedia article has slightly better variable names.
For part 1., take \(B = X\). Taking \(B = Y\) (as the author suggests) is incorrect because there’s no guarantee that \(Y ∈ \bf{Op}\).
For part 2. we know that \(Y\) is a member of \(\bf{Op}_{?∩Y}\) by part 1. and that ∅ is a member by taking \(B = ∅\).
We know that we have binary/finite intersections between any \(A_1, A_2\) because there must be some \(B_1, B_2\) such that \(A_1 = B_1 ∩ Y\) and \(A_1 = B_2 ∩ Y\). Since \(B_1 ∩ B_2 ∈ \bf{Op}\) because we have arbitrary intersections, we must have:
To show that we have arbitrary unions, we must show that given \(I\) as a set where we are given an open set \(A_i ∈ \bf{Op}_{?∩Y}\) for each \(i\) then their union \(⋃_{i∈I}A_i ∈ \bf{Op}_{?∩Y}\). We know that for every \(A_i\) there must be some corresponding \(B_i\) such that \(A_i = B_i ∩ Y\), so we can also write arbitrary unions of \(A_i\) as \(⋃_{i∈I}A_i = ⋃_{i∈I}(B_i ∩ Y) = (⋃_{i∈I}B_i) ∩ Y\). We know that \(⋃_{i∈I}B_i ∈ \bf{Op}\) because it has arbitrary unions, so \(⋃_{i∈I}A_i ∈ \bf{Op}_{?∩Y}\).
For part 3. we must show that for every \(B ∈ \bf{Op}\), the preimage \(f^{-1}(B) ∈ \bf{Op}_{?∩Y}\). Take any \(B\) that has no elements in common with \(Y\); the preimage will be ∅ ∈ \(\bf{Op}_{?∩Y}\). Otherwise the preimage \(f^{-1}(B)\) will be some open set \(A = B ∩ Y ∈ \bf{Op}_{?∩Y}\) that has all or a subset of the elements in \(B\).