7.2 Set as a topos#
from IPython.display import Image, IFrame


7.2.1 Set-like properties enjoyed by any topos#

Why does the author use ℰ (“script capital E” in Unicode) as a symbol for a topos? It’s not clear, but it will become common.
Limits and colimits#
The author will address all 5 items in the list above, but out of order. This section covers 1. and 2. together, then we’ll cover 4. then 3. then 5..
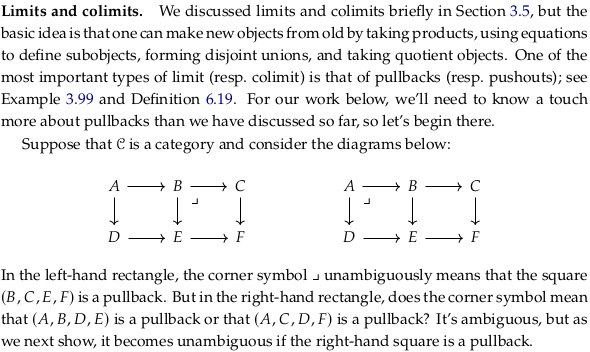
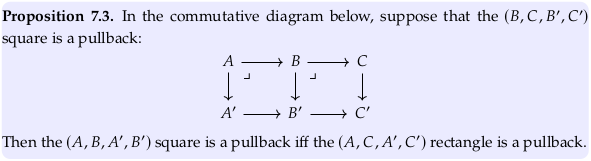
It’s not clear why the author changes the object labels in the proposition relative to the introduction to it. Either way, it’s not the case that \((A,B,D,E)\) (i.e. \((A,B,A',B')\) i.e. left square) being a pullback implies anything about \((B,C,E,F)\) (i.e. \((B,C,B',C')\) i.e. right square) being a pullback; these are completely separate questions. Proposition 7.3 is saying that if the right square is a pullback, then the left square is a pullback iff the whole rectangle is a pullback.
Exercise 7.4#
Notice both our answer and the author’s ignores the question’s appeal to use Definition 3.92.
The same proposition is given in Pullback (category theory) § Properties:
There is a natural isomorphism \((A×_CB)×_B D ≅ A×C_D\). Explicitly, this means:
if maps f : A → C, g : B → C and h : D → B are given and
the pullback of f and g is given by r : P → A and s : P → B, and
the pullback of s and h is given by t : Q → P and u : Q → D ,
then the pullback of f and gh is given by rt : Q → A and u : Q → D.
Graphically this means that two pullback squares, placed side by side and sharing one morphism, form a larger pullback square when ignoring the inner shared morphism:
Image('raster/2023-12-27T16-24-01.png', metadata={'description': "7S answer"})
Show code cell output

See also Exercise 7.4.
Epi-mono factorizations#

See also epi- (Wiktionary) and mono- (Wiktionary).

Define mono/epi-morphism#
The fact that these diagrams commute doesn’t teach us anything useful; we already knew that e.g. \(id_A⨟f = id_A⨟f\). Instead, let’s draw a second cone (one that is not the limit) over \(A→B←A\):
save_url = "https://q.uiver.app/#q=WzAsNSxbMiwyLCJBIl0sWzQsMiwiQSJdLFsyLDQsIkEiXSxbNCw0LCJCIl0sWzAsMCwiQyJdLFswLDEsImlkX0EiLDJdLFswLDIsImlkX0EiXSxbMiwzLCJmIiwyXSxbMSwzLCJmIl0sWzQsMCwidSIsMCx7InN0eWxlIjp7ImJvZHkiOnsibmFtZSI6ImRvdHRlZCJ9fX1dLFs0LDIsImdfMiJdLFs0LDEsImdfMSJdXQ=="
IFrame(src=f"{save_url}&embed", width="423", height="423")
This leads us to the more interesting fact that:
It’s this fact that we would not have if the diagram only commuted.
Said another way, the fact that \(f\) is a monomorphism (i.e. the diagram is a pullback) and that \(g_1⨟f = g_2⨟f\) implies that \(g_1 = g_2\). In the article Monomorphism this is the focus of the points around a monomorphism being a left-cancellative morphism (dually, an Epimorphism is right-cancellative). In this understanding, we collapse the \(id_A\) arrows into the \(A\) object. Renaming A/B/C to X/Y/Z:
Let’s call C/Z the vertex of the monomorphism \(f\) (being the vertex of the associated cone).
Exercise 7.6#

Image('raster/2023-12-27T19-59-00.png', metadata={'description': "7S answer"})
Show code cell output

See also Exercise 7.6.
Define pushing/pulling “along”#
See the text above Example 6.22 for comments on what it means for some morphism to be the pushout of \(g\) along \(f\). Presumably similar language is being used in Exercise 7.7 for pullbacks. It seems that when we say that \(x\) is the pullback/pushout of \(y\) along \(z\), we mean that we want to produce \(x\) from a parallel \(y\) on a diagram (with \(z\) connecting them). So \(x\) is like \(y\) but in some parallel world defined by \(z\).
For pullbacks, it seems that \(z\) connects the targets (for pushouts \(z\) connects the sources).
The same “pullback along” language was originally used in Exercise 1.79 and Example 1.117 for the same concept.
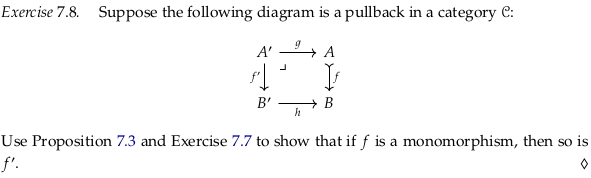
In the language of Pullback (category theory) § Properties what we are trying to prove in Exercise 7.8 is worded as:
Monomorphisms are stable under pullback: if the arrow f in the diagram is monic, then so is the arrow p₂. Similarly, if g is monic, then so is p₁.
The author could have worded Exercise 7.8 as asking whether the pullback of a monomorphism \(f\) along any morphism \(h\) is also a monomorphism.
Exercise 7.7#
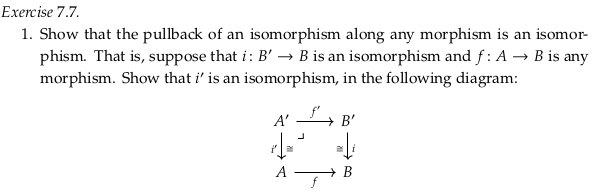
In the language of Pullback (category theory) § Properties what we are trying to prove here is worded as:
Isomorphisms are also stable, and hence, for example, \(X ×_X Y ≅ Y\) for any map \(Y → X\) (where the implied map \(X → X\) is the identity).
Image('raster/2023-12-27T21-49-09.png', metadata={'description': "7S answer"})
Show code cell output

Image('raster/2023-12-27T21-48-17.png', metadata={'description': "7S answer"})
Show code cell output

See also Exercise 7.7.
Exercise 7.8#
Image('raster/2023-12-29T16-13-03.png', metadata={'description': "7S answer"})
Show code cell output
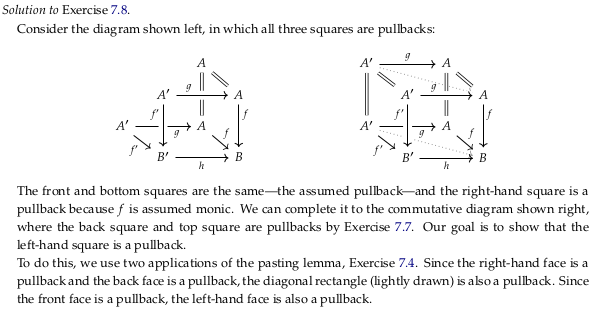
Notice the author’s mention of the Pasting lemma. See also Exercise 7.8.
See also How to prove that pullback preserves monomorphisms? - MSE and What does it mean for pullbacks to preserve monomorphisms? - MSE and the following from Monomorphism:
In the setting of posets intersections are idempotent: the intersection of anything with itself is itself. Monomorphisms generalize this property to arbitrary categories. A morphism is a monomorphism if it is idempotent with respect to pullbacks.
Epi-mono images#

See also Isomorphism theorems § Discussion.
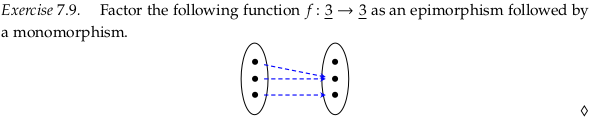
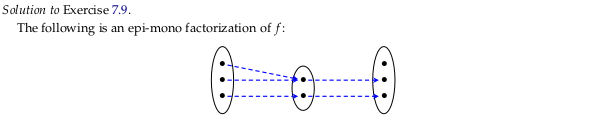
Exercise 7.9#
Image('raster/2023-09-13T16-30-42.png', metadata={'description': "7S answer"})
Show code cell output
Cartesian closed#

See also Cartesian closed category.
Exercise 7.11#



7.2.2 The subobject classifier#
Definition 7.12#

Special arrows#
See also Subobject classifier. It is strange the author uses ↣ for a monomorphism (i.e. adds a tail) for \(m\) but then does not for \(true\) (also a monomorphism). Per Exercise 7.8, showing it on the right would have implied it on the left.
According to quiver, the tail is appropriate for monomorphisms. According to category theory - Special arrows for notation of morphisms - MSE (2011 answers), it should be limited to inclusions. According to both Wikipedia and the MSE article, using a hook is an alternative syntax for both injections and monomorphisms.
Since it seems wasteful to have both the hook and the tail mean the same thing, we’ll follow the author and quiver and use a tail for a monomorphism (and leave a hook for an injection).
Everyone seems to agree that the two headed arrow is appropriate for epimorphisms, but What are usual notations for surjective, injective and bijective functions? - MSE defines the symbol only for surjections. We’ll use it for both; adding a symbol should generally also only make diagrams richer (as opposed to adding confusion).
Options for bijections:
Options for isomorpisms:
Subobject translator#

The subobject classifier in Set#

Exercise 7.16#
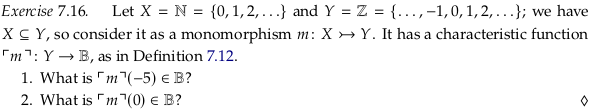
Image('raster/2023-10-24T14-26-59.png', metadata={'description': "7S answer"})
Show code cell output
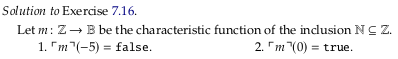
Exercise 7.17#

Image('raster/2023-10-24T14-38-05.png', metadata={'description': "7S answer"})
Show code cell output

7.2.3 Logic in the topos Set#



Exercise 7.19#

Image('raster/2023-10-24T18-27-50.png', metadata={'description': "7S answer"})
Show code cell output

Exercise 7.20#

Image('raster/2023-10-24T19-02-36.png', metadata={'description': "7S answer"})
Show code cell output

Exercise 7.21#
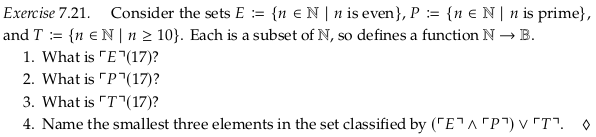
Image('raster/2023-10-24T19-07-16.png', metadata={'description': "7S answer"})
Show code cell output

Review#
