4.4. Categorification#

See also Categorification. This process is about asking where something came from. It’s creative; in the sense of imagination being better than knowledge it asks you to come up with many possible models, many possible worlds, such as the quantum mechanics model. It’s telling an origin myth (aition) in terms of mathematics. As the author mentions there is no bottom, just like there is no end to the turtles in the classic aition. From the Wikipedia article:

Categorification and decategorification are not precise mathematical procedures, but rather a class of possible analogues. They are used in a similar way to the words like ‘generalization’, and not like ‘sheafification’.

4.4.1. The basic idea of categorification#

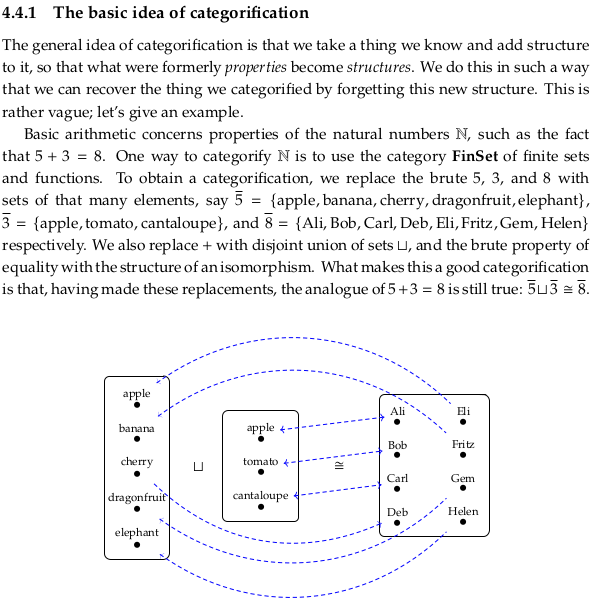
4.4.2. A reflection on wiring diagrams#

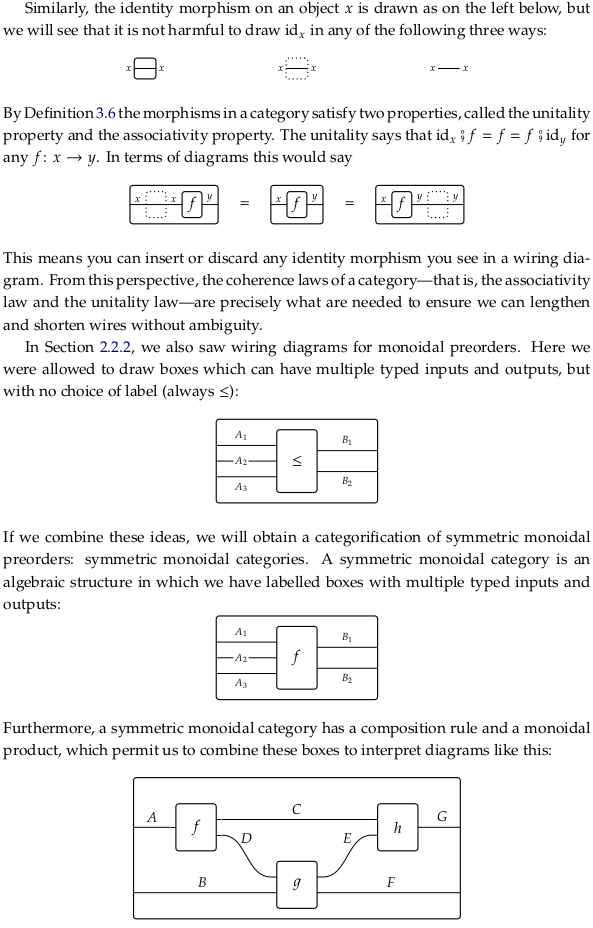
4.4.3. Monoidal categories#

Rough Definition 4.45.#

See also Monoidal category, though we’ve jumped to Symmetric monoidal category (see also symmetric monoidal category). What makes this definition “rough” is that the author has decided to ignore all the coherence conditions (triangle, pentagon, hexagon, etc.).

Exercise 4.48.#

Let’s recall the definition:

The (i) constituent roughly remains the same, with a singular identity “element” replaced by an identity “object” (such as a singleton set). An object here is a generalization of an element.

In (ii) we generalize a function for ⊗ to a functor. This functor ⊗ is from 𝓒 × 𝓒 → 𝓒, where 𝓒 is a preorder. The left hand side of this functor (𝓒 × 𝓒) is a product of preorders (see Example 1.56) where \((p₁,p₂) ≤ (q₁,q₂)\) if \(p₁ ≤ q₁\) and \(p₂ ≤ q₂\). So for ⊗ to be a functor (preserve composition) i.e. a monotone map we must have that whenever \((p₁,p₂) ≤ (q₁,q₂)\) (i.e. \(p₁ ≤ q₁\) and \(p₂ ≤ q₂\)) we also have \(p₁⊗p₂ ≤ q₁⊗q₂\). This is exactly the requirement of (a) in Definition 2.2. The same point is made in Monoidal category § Monoidal preorders under:

Furthermore, the fact that · is required to be a functor means—in the present case, where C is a preorder—nothing more than the following:

if \(c_1\to c_1'\) and \(c_2\to c_2'\) then \((c_1\cdot c_2)\to (c_1'\cdot c_2')\)

Part (b) of Definition 2.2. is generalized from two equations to the two natural isomorphisms listed in (a) and (b) in Rough Definition 4.45. That is, we must add two natural isomorphisms to allow for “flexibility” in how I ⊗ c is “equivalent” to c. Said another way, these two objects are equivalent “up to isomorphism” i.e. only with ≅ rather than =. For an example of this with respect to identities see the last paragraph of Example 4.49.

Part (c) of Definition 2.2. is again generalized from a single equation to a single natural isomorphism in part (c) of Rough Definition 4.45. An example of this is discussed in the paragraphs above Rough Definition 4.45.

Part (d) of Definition 2.2. is again generalized from a single equation to a single natural isomorphism in part (d) of Rough Definition 4.45.

Example 4.49.#

Exercise 4.50.#

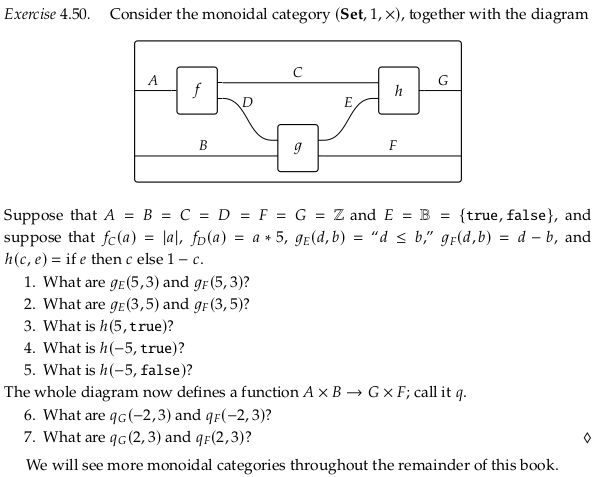
f_C = lambda a: abs(a)
f_D = lambda a: a*5
g_E = lambda d,b: d <= b
g_F = lambda d,b: d - b
h = lambda c,e: c if e else 1 - c

g_E(5,3), g_F(5,3)

(False, 2)

g_E(3,5), g_F(3,5)

(True, -2)

h(5,True)

h(-5,True)

-5

h(-5,False)

q_G = lambda a,b: h(f_C(a), g_E(f_D(a), b))
q_F = lambda a,b: g_F(f_D(a), b)

q_G(-2,3), q_F(-2,3)

(2, -13)

q_G(2,3), q_F(2,3)

(-1, 7)

4.4.4. Categories enriched in a symmetric monoidal category#

Rough Definition 4.51.#

Exercise 4.52.#

Let’s recall Definition 3.6:

The constituent (i) is the exact same between the two definitions. The constituent (ii) is a simple generalization in Rough Definition 4.51; when we apply 𝓥 = (Set, {1}, ×) the hom-object becomes a hom-set.

Regarding (iii), in Definition 3.6 the identity morphism was part of the set \(\mathcal{X}(x,x)\) and conceptualized as being on \(x\). In Rough Definition 4.51 it’s a morphism in 𝓥 = (Set, {1}, ×) from {1} to \(\mathcal{X}(x,x)\). A morphism in Set is a function. A function from {1} to some (presumably larger) set then “selects” an object from that set, in this case selecting one morphism from a set of morphisms.

It looks like (iv) is essentially the same. In Definition 3.6 we enumerate all morphisms \(f\) and \(g\) associated with three objects, while in Rough Definition 4.51 we take the cartesian product of all morphisms between the first/second and second/third objects. We should get the same answer either way.

Remark 4.53.#

Recalling the definition:

Exercise 4.54.#

In a Cost-category the identity element and the top element are the same: 0. The identity elements of a category enriched in Cost are \(id_x: I → \mathcal{X}(x,x)\) or when specializing to a preorder the arrows \(I \leq \mathcal{X}(x,x)\). As explained in the text above this exercise, a preorder always has at most one morphism between any two objects. The \(I \leq \mathcal{X}(x,x)\) requirement is effectively that there is one element rather than zero.

The requirement that \(I \leq \mathcal{X}(x,x)\) in Definition 2.46 translates to \(0 \geq \mathcal{X}(x,x)\) in a Cost-enriched category because Cost = ([0,∞],≥,0,+). In Cost there are no arrows up from the top however. This constrains the \(id_x\) for all \(x\) to the identity element on zero in Cost; this is the only morphism from the \(I\) in Cost (i.e. 0) to any other element in Cost.

Conceptually, it makes sense that the distance from any object to itself is zero.

Reveal 7S answer

4.4. Categorification

Contents