Exercise 7.7

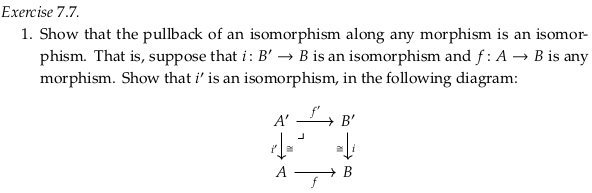
To show that \(i'\) is an isomorphism, we must show that \(i'⨟q = id_{A'}\) and \(q⨟i' = id_A\) for some morphism \(q\). How do we come up with any morphism \(q: A→A'\), much less one that is an inverse? If \(A\) was the vertex of a cone over \(A→B←B'\) then we could use the universal property of the pullback to generate at least one morphism. It is in fact a cone; the outer square in the following diagram commutes because \(id_A⨟f = f⨟i^{-1}⨟i = f\):

So we’ve generated some \(u\) that may be able to serve as the inverse \(q\) we are looking for. Because of the universal property:

\[\begin{split} \begin{align} u⨟i' & = id_A \\ u⨟f' & = f⨟i^{-1} \end{align} \end{split}\]

We can ignore the second equation, but the first equation is half of what we are trying to show. How do we also show that \(i'⨟u = id_{A'}\)? Recall that \(A'\) is also a cone over \(A→B←B'\), and in fact the limiting cone:

This means that there is at most one morphism from \(A'\) to \(A'\) where the source (\(A'\)) is also a cone over \(A→B←B'\). The morphism \(i'⨟u\) exists simply by composition and is also from \(A'\) to \(A'\), and so must equal \(id_{A'}\).

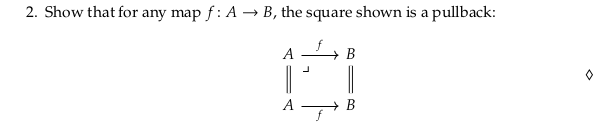
It’s trivial to show the diagram commutes: \(id_A⨟f = f⨟id_B\). We must also show that for any \(m: C→B\) and \(n: C→A\) where the outer square in the following diagram commutes (i.e. \(n⨟f = m⨟id_B\)) there exists a unique morphism \(u: C→A\) so that \(u⨟f = m\) and \(u⨟id_A = n\):

The morphism \(n\) already satisfies the two equations and so can serve as \(u\).