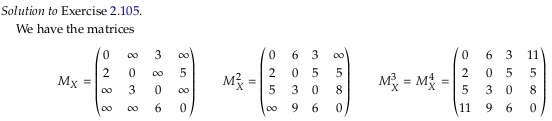2.5. Quantale matrix multiplication#
from IPython.display import Image

2.5.1. Monoidal closed preorders#

Definition 2.79#

Define closed monoidal preorder#
We prefer the language “closed monoidal preorder” to “monoidal closed preorder” (the title of this section) only because it’s more common. See closed monoidal category and Closed monoidal category.
An equation equivalent to (2.80) is given at the start of Heyting algebra. The reasoning behind the choice of ⊸ (named multimap in the unicode standard, or \multimap in latex) for Heyting implication is mentioned in Heyting algebra § Category-theoretic definition. Per Heyting algebra § Formal definition, this symbol could perhaps more meaningfully be referred to as the Relative pseudocomplement.
Later, with the background of Chp. 3, read Closed category for a better explanation of how categories of this type enrich themselves. It looks like the author is defining the word “hom-element” as the hom-set for the category; perhaps because preorders have at most one element in their hom-set we can get away with this. See also the paragraph under Equation (7.10).
See also Brouwer–Heyting–Kolmogorov interpretation. As indirectly made more explicit in bhk-interpretation.pdf, the notation 〈0,a〉 and 〈1,a〉 are being used here in the sense of a disjoint union (categorical sum) and the meet corresponds to a categorical sum.
Exercise 2.82.#

See also Exercise 2.82.
Image('raster/2023-10-28T18-37-34.png', metadata={'description': "7S answer"})
Show code cell output

Example 2.83.#

We start with:
Subtracting \(x\) from both sides:
Applying \(max(0,-)\) to both sides:
Let’s say we know that \(a + x ≥ 9\) i.e. that some part of our project will cost at least 9 (a lower bound). We can then conclude that \(a ≥ x ⊸ 9\) i.e. that \(a ≥ max(0, 9 - x)\), or equivalently that \(x ≥ max(0, 9 - a)\). This is the approach of allocating some resources for a task and seeing how it could be split up.
Let’s say we instead know that \(a = 3\). If we also know that \(a + x ≥ y\), then we can conclude that \(3 ≥ x ⊸ y\) or that \(3 ≥ max(0, y - x)\). That is, given \(3\) we can give you a “single use v-to-w converter” i.e. the inequality \(3 ≥ max(0, y - x)\) that could be used to determine an upper bound on \(y\) given \(x\). That is, using (2.80) we can conclude that \(3 + x ≥ y\) (essentially going back to where we started).
Let’s switch to the variable names of (2.80) and use part (c) of Proposition 2.87. If you have a \(v\) (a cost) and a \(v ⊸ w\) (roughly, a cost difference), you can get a \(w\) (minimum cost) via \(v + max(0, w - v) ≥ w\).
Exercise 2.84.#
See also Exercise 2.84.
Image('raster/2023-10-28T18-38-09.png', metadata={'description': "7S answer"})
Show code cell output


Proposition 2.87#


Remark 2.89: Self-enriched#

Some examples of categories enriched in themselves (i.e. closed):
Bool-category Bool
Cost-category Cost
Set-category Set
See also Enriched category; any Closed monoidal category is enriched in itself.
2.5.2. Quantales#
Definition 2.90.#

Define quantale#
See Quantale. A unital commutative quantale is a symmetric monoidal closed preorder that has all joins. A unital quantale is a monoidal closed preorder that has all joins. This corresponds to the following alternative definition from the Wikipedia article:
A unital quantale may be defined equivalently as a monoid in the category Sup of complete join semi-lattices.
The primary definition used by the Wikipedia article (based on a distributive property) is discussed in Proposition 2.98 below.
If we strip the term “unital” from quantale we wouldn’t be able to call the preorder “monoidal” anymore because that would require unitality. A monoid without an identity element is a semigroup; the term semigroup isn’t used too often because it’s easier to say a set that has nothing but a closed (see Magma (algebra)) associative binary operation. The Wikipedia article includes this definition by saying they are sometimes called complete residuated semigroups.
At a high level the term “quantale” brings together order theory and basic algebraic structures.
The concept of a quantale is closely tied to binary relations. See Relation algebra and Algebraic logic / Calculus of relations and this comment.
Example 2.91: Cost quantale#

See also Exercise 2.40.
Exercise 2.92: Bottoms and joins#

Image('raster/2023-10-28T18-39-50.png', metadata={'description': "7S answer"})
Show code cell output

Exercise 2.93: Bool quantale#
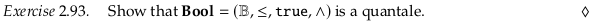
See also Exercise 2.93.
Image('raster/2023-10-28T18-38-44.png', metadata={'description': "7S answer"})
Show code cell output

Exercise 2.94: Power set quantale#
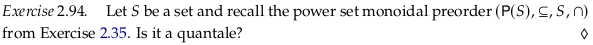
See also Exercise 2.94.
Image('raster/2023-10-28T18-39-04.png', metadata={'description': "7S answer"})
Show code cell output

Remark 2.95#

Proposition 2.96#
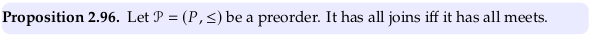

This proof is tricky; see Joins and Meets in Preorder - Mathematics Stack Exchange for a question specific to it and this text. To “have all joins” doesn’t mean (as in the definition of a Semilattice) that a join exists for any nonempty finite subset. That is, a semilattice has all nonempty joins. A preorder that has all joins has all joins in the sense of Definition 2.90 here; a join exists even for the empty set. A preorder has all joins if it has a bottom element, which can obviously always serve as the meet of any subset that would otherwise not have one. The author intends to restrict quantales to being based on a preorder that is a Complete lattice.
The same issue is discussed in Completeness (order theory) § Least and greatest elements. Even with that out of the way, this proof has issues. A better proof comes from Completeness (order theory) § Relationships between completeness properties:
The best-known example is the existence of all suprema, which is in fact equivalent to the existence of all infima. Indeed, for any subset X of a poset, one can consider its set of lower bounds B. The supremum of B is then equal to the infimum of X: since each element of X is an upper bound of B, sup B is smaller than all elements of X, i.e. sup B is in B. It is the greatest element of B and hence the infimum of X. In a dual way, the existence of all infima implies the existence of all suprema.
Remark 2.97#

See also Hausdorff distance.
Proposition 2.98#

2.5.3. Matrix multiplication in a quantale#

Why is it necessary to be closed and have all joins to support matrix multiplication? The general definition of matrix multiplication uses joins, i.e. they seem to be required by how we choose to define our general form of matrix multiplication. It’s likely that being closed is necessary so that we have the distributive law as in Eq. (2.88).


See also Two-element Boolean algebra and Boolean matrix.

Exercise 2.103.#
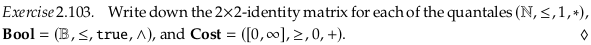
Image('raster/2023-10-28T18-42-25.png', metadata={'description': "7S answer"})
Show code cell output

Exercise 2.104.#

See also Exercise 2.104.
Image('raster/2023-10-28T18-44-08.png', metadata={'description': "7S answer"})
Show code cell output




Exercise 2.105.#

See also Exercise 2.105.
Image('raster/2023-10-28T18-44-40.png', metadata={'description': "7S answer"})
Show code cell output