Exercise 2.84

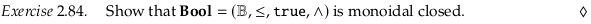
We’ll assume we don’t know the hom-element \(v⊸w\) is \(v→w\) i.e. \(w∨¬v\). The second-to-last column is then what we could allow it be defined as, and the final column is how we choose to define it:

One could read (2.80) in this context as the rule that if \(a\) and \(v\) holding means that \(w\) also holds, then it’s also the case that \(a\) holding means that if \(v\) holds then \(w\) holds. In terms of wiring/string diagrams (visual proofs):

In the category of sets this becomes Currying:

If you have a \(v\) (know it holds) and a \(v ⊸ w\) (know it holds), you can get a \(w\) (conclude it holds) via \(v ∧ (w∨ ¬v) = v ∧ w ≤ w\).