3.4. Adjunctions and data migration#

3.4.1. Pulling back data along a functor#


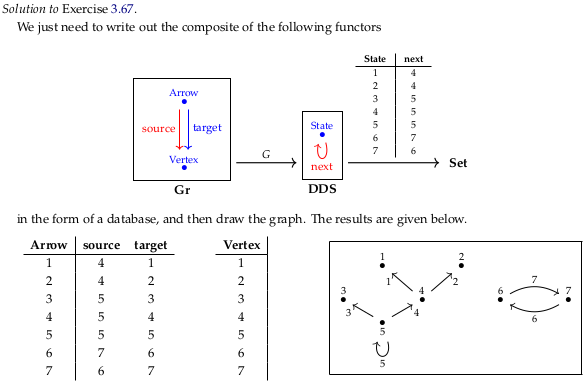
Exercise 3.67.#

Every arrow indicates “this is the state that I came from” (the source). You could use this diagram to work back to how you could have gotten to some final state:
Reveal 7S answer
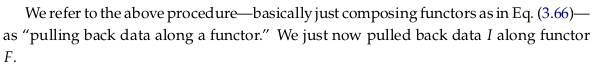

3.4.2. Adjunctions#

Definition 3.70.#


Read through Adjoint functors and in particular the section Definition via Hom-set adjunction for a more detailed version of this definition. Unfortunately, the Wikipedia article describes the left adjoint from 𝓓 → 𝓒 (opposite the authors). You’ll have to switch these two letters everywhere to read it. In particular, this switch implies the objects X in the Wikipedia definition correspond to the objects d in the author’s definition (and the objects Y correspond to the objects c). In the diagram in Wikipedia’s defintion, you’ll need to switch the morphisms f and g, as well as reflect the whole diagram across a vertical line in the center of the diagram.
If two morphisms are inverses, then \(f⨾g = id_A\) and \(g⨾f = id_B\), and we say that A and B are isomorphic objects. We call \(f\) more specifically an “isomorphism” rather than a morphism. We call \(f\) and \(g\) “inverses” but more specifically they are inverse morphisms (or “object” isomorphisms) (not inverse functors, which act between categories).
See instead Remark 3.59 and the concept of an Equivalence of categories for examples of “inverse” functors. Strictly speaking, an equivalence of categories only requires that isomorphic objects in the first category correspond to isomorphic objects in the second category (think of a map between preorders rather than partial orders). An Isomorphism of categories would require a “true” inverse functor.
An adjunction relaxes the concept of “inverse” even more than an equivalence of categories does. It complicates the concept of a Hom-functor (a single bifunctor) by effectively introducing two bifunctors (that now act on different categories) to the category of sets. The category of sets provides a “middle ground” that is used to define a natural relationship.
Example 3.71.#

Example 3.72.#

See also Exponential object.
Exercise 3.73.#

For 3. we are defining a new function that adds 3. That is, p(3) := (b) ↦ 3 + b
Reveal 7S answer

Example 3.74.#

3.4.3 Left and right pushforward functors, Σ and Π#
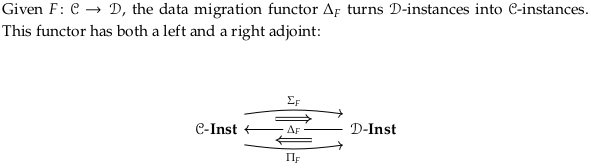
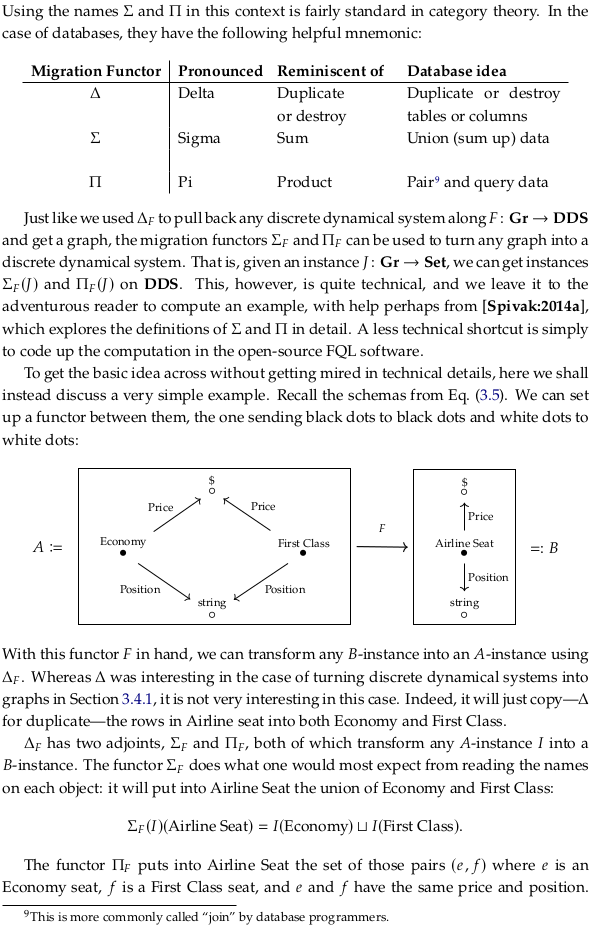

3.4.4. Single set summaries of databases#

Exercise 3.76.#
This functor sends all objects to the object 1 and all morphisms to id₁.
Reveal 7S answer


Exercise 3.78.#
Reveal 7S answer

