3.5. Bonus: limits and colimits

3.5.1. Terminal objects and products

Exercise 3.81.

No object in the preorder will have a unique morphism for every object C in 𝓒 to it, except the top object, because there will be no morphism at all from the top object to it. The top object will be a terminal object because every other object in a preorder will have only one morphism to it (there is at most one morphism between any two objects in a preorder category).

Reveal 7S answer

Exercise 3.82.

The category 1. In Cat the objects are categories and the morphisms are functors, and there will be one unique functor “!” to every category as given in Eq. (3.75).

Reveal 7S answer

Exercise 3.83.

The category with two objects and two parallel morphisms between them. There are only two candidate objects for the terminal object. The object with two morphisms into it is not the terminal object because there is no unique morphism from it to the other object (there are zero morphisms). The object with two morphisms out of it is not the terminal object because there are two morphisms to the other object rather than one.

Reveal 7S answer

Proposition 3.84.

Definition 3.86.

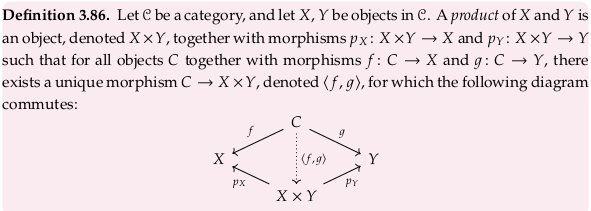
For the ∃! in the drawing, see Uniqueness quantification. See Universal property § Examples § Products for a similar definition. How does this article’s commutative diagram relate to the author’s? Redrawing the commutative diagram provided in the text:

Doubling up the objects/morphisms so we can “fold” the right wing onto the left wing:

Flipping the diagram and using notation from the Wikipedia article:

Notice the conflict in language between the author and the article as well; what has a universal property? In the text, objects (terminal objects, product objects) have a universal property. In the Wikipedia article, universal morphisms (an object/morphism pair) have the universal property. It seems the Wikipedia article wants to define a globally unique object/morphism pair, which isn’t really possible with just an object. See Remark 3.85 or equivalently Why are two universal objects isomorphic? - Mathematics Stack Exchange. That is, there can be two universal objects, but there is really only one of each object/morphism pair.

See universal - Wiktionary. The term “universal” in this context means “useful for many purposes” in the sense that the universal object is useful like a universal wrench. The universal object or universal object/morphism is by no means common to all members of the set.

Exercise 3.88.

Only the elements c in 𝓒 where c ≤ x and c ≤ y are candidates for the product of x and y because they are the only elements that will have a \(p_X\) and \(p_Y\) (in the language of Definition 3.86) that point to x and y. These other elements will not satisfy the definition of a product, however, because there will be no \(〈f,g〉\) between the element and the meet x ∧ y (since the meet is the greatest element that is less than both x and y). That is, there an arrow from c → x×y in the following diagram, but no arrow in the reverse direction:

For the meet x ∧ y, the \(〈f,g〉\) morphism is the only morphism that exists between all the lesser elements and it. In a preorder there is at most one morphism between objects, so to call the arrow c → x×y “unique” (or to make it dashed/dotted) is potentially confusing.

Reveal 7S answer

Example 3.89.

• Example 3.86: Product (category theory), or “categorical product” for short.

• Example 3.89: Product category

Exercise 3.90.

The identity morphisms in a product category are the pairs of identity morphisms in the two composing categories.

Composition in a product category is associative because composition in each of the composing categories is.

The product category 1 × 2 has two objects (1,1) and (1,2). The only non-identity morphism is \((id_{1}, p_{12})\).

The product category when P and Q are preorders is the “product” preorder, as described in Example 1.56. and Exercise 1.57.

Reveal 7S answer

3.5.2. Limits

Prerequisite to Cone (category theory), which is prerequisite to Limit (category theory). Notice the latter article uses \(L\) in the text and commutative diagrams for the limit (which is a cone).

Dotted, dashed, and unique to

In Universal property and other articles, the unique morphism that exists because of some universal property is typically dashed. The author uses dotted lines in Definition 3.86 because he has already committed to using dashed lines for functors between categories. Later he’ll use dashed lines. These two kinds of arrows often have to show up on the same diagrams, in which case we’ll use dotted arrows for unique morphisms (see e.g. Free object).

What’s more of a problem is how the word “unique” is thrown around in both online articles and the text, and the first paragraph of this section highlights the conflict: why is the “unique” map \(C → X×Y\) associated with the product not sufficient to qualify as the “unique” morphism required of a terminal object in Definition 3.79? Why isn’t a product already a terminal object?

See unique - Wiktionary. In the definition of a terminal object, we’re using the term “unique” to mean “Being the only one of its kind” (the first definition of the word). In the definition of a product object, we’re using the term “unique” to mean “Particular, characteristic” or said another way, we mean to say the morphism is unique to some other morphism. When we move to the category of cones, the product cone will become “unique” in the global sense.

Said another way, see Initial and terminal objects. In this context “unique” means the the cardinality of the set of morphisms between the two objects is one, no more or less.

It’s easy to verify this by looking at e.g. the diagram at the bottom of Example 3.87. The diagram indicates ∃! (there exists a unique map) from C to the product category. But clearly, there is not just one map from an arbitrary set (e.g. {1,2,3}) to a product category. The morphism in this diagram is unique to \(f\) and \(g\).

Said another way, there is a one-to-one mapping (a bijection) between these morphisms. The language “one-to-one” is used in e.g. Exercise 5.23 later in the text (the author uses “one-to-one correspondence” frequently, apparently always for a bijection). Because we’re usually working with regular categories (Set-categories) the hom-objects are sets and these bijections are actually between sets. From universal construction in nLab:

For example, if one were asked to give a map \(\mathbb{R} \to \mathbb{R} \times \mathbb{C}\), they might write down something like \(x \mapsto (x^2, x + i x)\). In effect, what is done is that a pair of maps \(\mathbb{R} \to \mathbb{R}\) and \(\mathbb{R} \to \mathbb{C}\) is given, namely \((x \mapsto x^2, x \mapsto x + i x)\). The universal property of the product says that giving a map to \(A \times B\) is the same as giving a map to \(A\) and a map to \(B\), and moreover this correspondence is natural in some precise sense.

…

For it to be a universal property, just the existence of such a bijection is not sufficient. We will need some conditions to make sure the bijection is “natural”. Abstractly, this says that the bijection is given by a natural isomorphism of certain functors.

The fact that the commutative diagram “commutes” over the whole category is what leads to this bijection. When we move to the category of cones, where you can think of each of the objects as commutative diagrams, then you may notice that one commutative diagram (one object) is special or stands out among all the rest.

Whenever you see someone say “For any … there exists a unique” (as in Universal property) (as in the start of this section) you can probably shorten their language to “unique to” in one way or another.

Exercise 3.91.

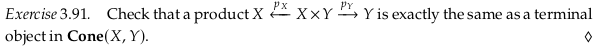
Notice the symmetry between the last diagram of Definition 3.86 and the diagram immediately above Exercise 3.91; both of these diagrams depict two cones but with different labels on the graph elements. In the first, we are claiming that for all cones centered on C there is a unique morphism to the cone centered on the product X × Y. Thinking in terms of a terminal object in Cone(X,Y), this is equivalent to claiming that there exists a unique morphism !: C → Z = (X ← X × Y → Y) which is referred to as 〈f,g〉 for each object C of 𝓒.

Reveal 7S answer

Definition 3.92.

Example 3.87 is Definition 3.92 where D specifically points to the objects \(X=\{1,2,3,4,5,6\}\) and \(Y=\{1,2,3,4\}\) in 𝓒 = Set. While 𝓙 may be abstract (the whole indexing category), D is a functor that points to specific objects in 𝓒. This can be confusing if you conflate D with 𝓙. The category Cone(D) is defined for a specific functor; in Example 3.87 the categorical product in 𝓒 is the terminal object in Cone(D) but there are many other cones. Looking at Example 3.94, there are also many diagrams D that can be defined where the indexing category 𝓙 is as given.

It can be tempting to think that two indexes are necessary; one that indexes the objects in 𝓙 and one that indexes all the ways that 𝓙 can map onto 𝓒. The former index is not necessary; we don’t index objects. There are two levels of indexing in some sense, however. The first is less so indexing, but you can think of a one-to-one map between all the possible categorical products in 𝓒 and diagrams D. The category Cone(D) provides a second level of indexing (many cones). That is, there are many categories Cone(D) all defined for many diagrams D, with each having only one terminal object.

In the last paragraph, the term “projections” is chosen with products in mind. See the picture at the bottom of Example 3.87 for a visualization; the product relation (the 2-d box) can be “projected” into either X or Y (the 1-d lines).

Define categorical limit

You’re likely already using the term limit in the sense of Limit (mathematics). Per that article the concepts are related:

The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory.

See also Limit § Mathematics.

3.5.3. Finite limits in Set

It’s possible to get through the next two exercises (and this chapter) without understanding what is meant by the constraints on the arrows. See Example 3.99 for at least a basic introduction to them.

In some sense, this is a strange definition. It asks you to provide an example diagram for 𝓙 rather than working directly from 𝓙 and the category. This captures the idea behind the word “limit” however; given an example diagram we can “take it to the limit” to get some unique object. Given a similar example, we could have constructed the same limiting object.

Exercise 3.97.

Call \(v\) and \(w\) in the diagram in Example 3.94 \(v_1\) and \(v_2\) to make that application of the definition easier. With this, it’s easier to see how the set-builder notation being used in Theorem 3.95 boils down to the set-builder notation used at the start of Example 3.87 (notice \(A\) is empty).

Reveal 7S answer

Exercise 3.98.

Call the one element in \(1\) by \(v_1\) to make the application of the definition easier, and use the name \(X\) for the target of the functor D. The limit is just the set itself. Looking at Definition 3.92 one can think any other set that has the set \(X\) as the codomain (target) as a cone in Cone(D), and the projection map of the limit as \(id_X\).

The author provides no answer to this question in the appendix (presumably assuming you can check your answer against Definition 3.92).

Example 3.99.

Prerequisite to Pullback (category theory).

Somewhat confusingly, the variables \(f\) and \(g\) are reused (by being mapped to themselves) in this example. That is, \(D(f)\) (where \(f\) refers to the \(f\) in the cospan graph) equals \(f: \underline{6} → A\), and \(D(g) = g: \underline{4} → A\). That officially makes the limit, in Set-builder notation:

\[ lim_𝓙 D ≔ \{(x,a,y)|x∈X,a∈A,y∈Y,f(x)=a,f(y)=a\} \]

Why does the author call the diagonal arrow \(c_a\) superfluous? Perhaps because composition is always possible in a category; you can always compose e.g. \(c_y⨟g\) to get some other morphism. You can call what you want (i.e. give it a separate name), and you can draw it on the diagram if you want. This is similar to how in a preorder there is technically a single morphism between e.g. the top and bottom element despite there being many paths in-between. You could draw all those extra direct paths, but it would clutter the drawing. Generally speaking, however, the most-factored names are going to be the most useful, so given the following three equivalent statements we’ll likely use only the first or third:

\[ c_x⨟f = c_a = c_y⨟g \]

Regardless, the suggestion that we name the cone point and add the ⌟ symbol only because the diagram commutes is incorrect. To be a pullback, we can’t just have a commutative square. The pullback \(X×_AY\) must also be universal with respect to this diagram (and as a limit, not a colimit).

3.5.4. A brief note on colimits

Exercise 3.101.

We can have \(F^{op}\) map the same objects and morphisms to the same objects and morphisms that \(F\) did.

Reveal 7S answer

Definition 3.102.

3.6. Summary and further reading

See also Coherence condition.