Exercise 2.104

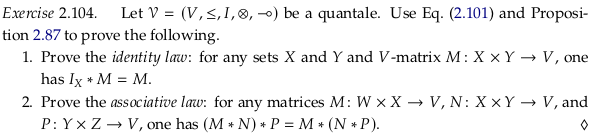
For 1. we have:

\[\begin{split} (I * M)(w,y) ≔ \bigvee_{x \in X} I(w,x) \otimes M(x,y) \\ (I * M)(w,y) ≔ I(w,w) \otimes M(w,y) \vee \bigvee_{x \in X \setminus \{w\}} 0 \otimes M(x,y) \end{split}\]

Using Definition 2.2. part (a), any \(0 \otimes x\) term is always \(0\), so this reduces to:

\[ (I * M)(w,y) ≔ M(w,y) \]

For 2. we have:

\[ ((M * N) * P)(w,z) = \bigvee_{y \in Y} \big( \bigvee_{x \in X} M(w,x) ⊗ N(x,y) \big) ⊗ P(y,z) \]

Using symmetry, part (b) of Proposition 2.87, and symmetry again:

\[ ((M * N) * P)(w,z) = \bigvee_{y \in Y} \bigvee_{x \in X} M(w,x) ⊗ N(x,y) ⊗ P(y,z) \]

Pulling out \(M(w,x)\) with part (b) of Proposition 2.87 again, we have:

\[ \bigvee_{x \in X} M(w,x) ⊗ \big( \bigvee_{y \in Y} N(x,y) ⊗ P(y,z) \big) = (M * (N * P))(w,z) \]